数据和数据维度
Dimension 维度
In simple words, the Axis is something that represents the dimension of data.
定义0维数据为标量,定义1维数据为向量,定义2维数据为矩阵. 常见的示例如下:
- 0维数据:标量,可以理解单独一个元素
1维数据:向量,可以理解为一个列表,如一个班级同学的姓名
这里有个例子,一个班级有五个人:

2维数据:矩阵,常见于数据集
形式与示例如下
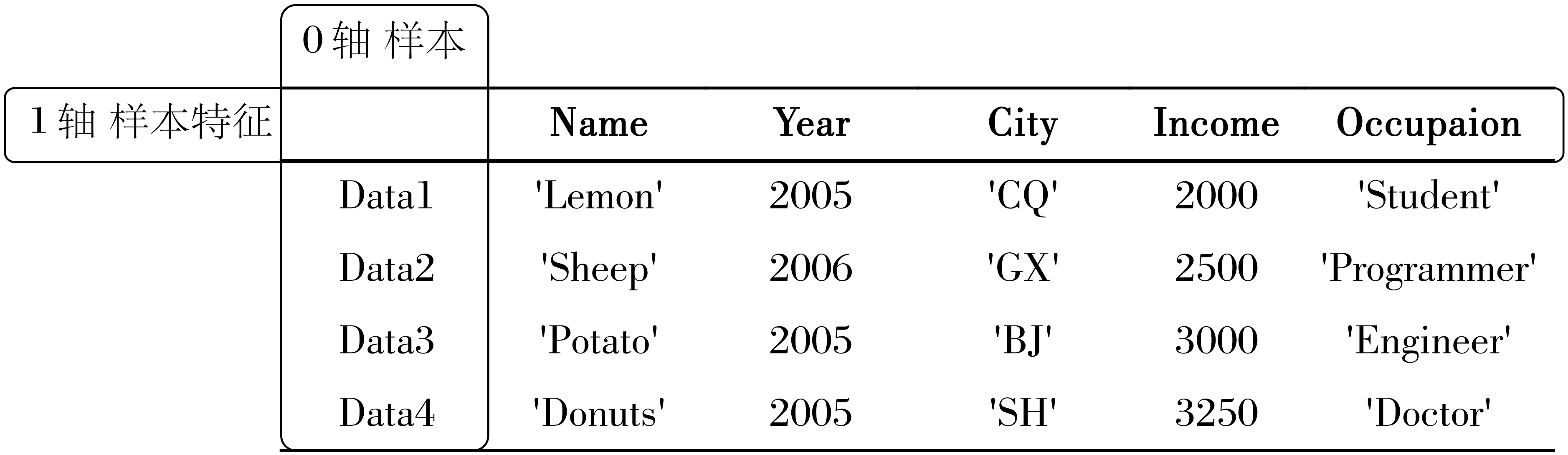
3维数据:通常用于存储含有序列特征的数据
示例如下(每年的新生采访表)
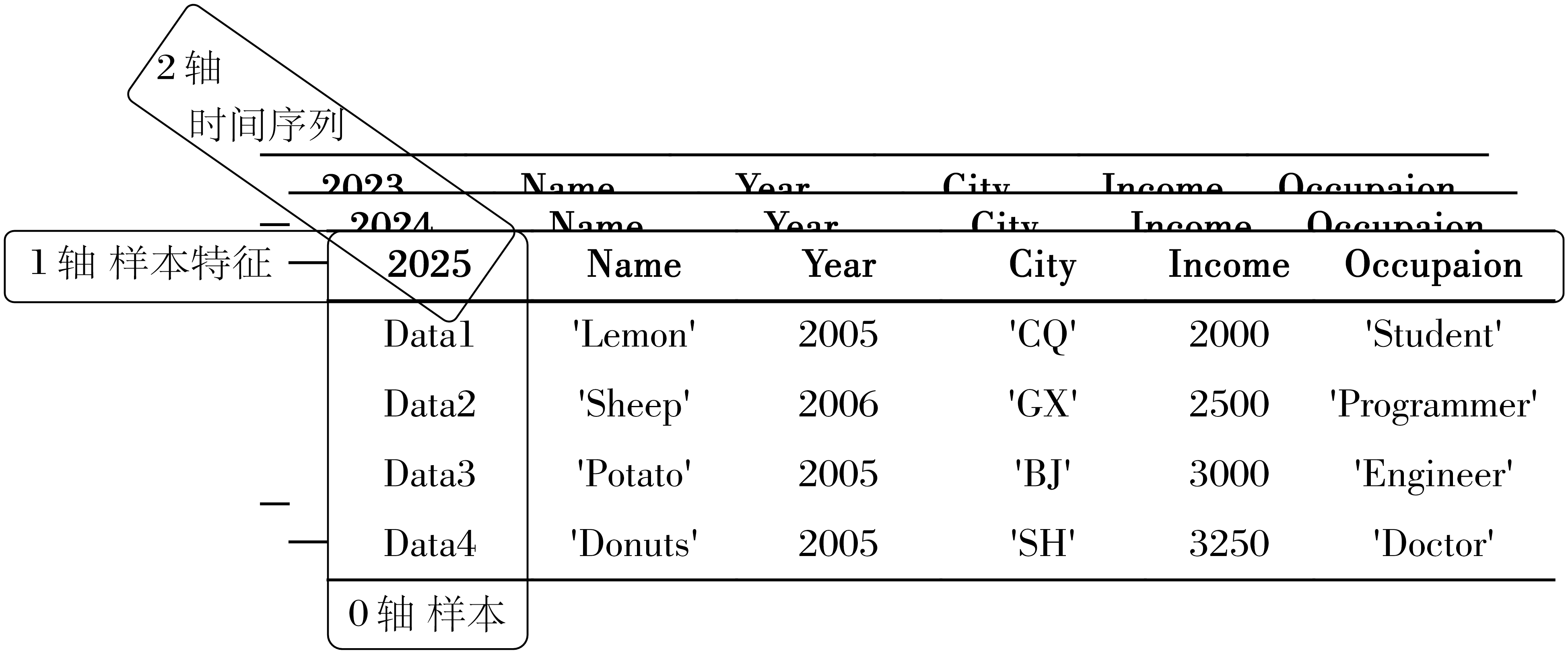
多维数据计算
NumPy库提供了多维数组ndarray,其中有些要注意的事项:
- N-Dimensional Array,N维数组
- 多维数组应由相同数据类型的元素组成
- 数组大小需事先指定
接下来一起在vscode里试试叭→
案例分析 1
5位学生参与了学业水平测试,测试科目牢7门,如下:
然后探讨下面3个任务:
Task 1 创造一维数组分别保存学生姓名和考试科目,访问数组元素
Task 2 数组元素的索引与一维数组的访问
Task 3 根据条件筛选数组元素
Task 1
常用
np.array()来基于列表创建一维数组# Code 01 import numpy as np name_list = ['Lemon','Sheep','Potato','Donuts','Tatari'] subject_list = ['Math','English','Python','Chinese','Art','Database','Physics'] print(name_list[1:3]) #复习了下索引左闭右开 names = np.array(name_list) subjects = np.array(subject_list) print('{}\n{}'.format(names,subjects))运行结果会抛出两个一维的NumPy数组(即一维ndarray)
['Lemon' 'Sheep' 'Potato' 'Donuts' 'Tatari'] ['Math' 'English' 'Python' 'Chinese' 'Art' 'Database' 'Physics']Task 2
与列表索引类似,这里数组的索引范围范围[0,n-1]or[-n,-1],其中n为一维数组的大小
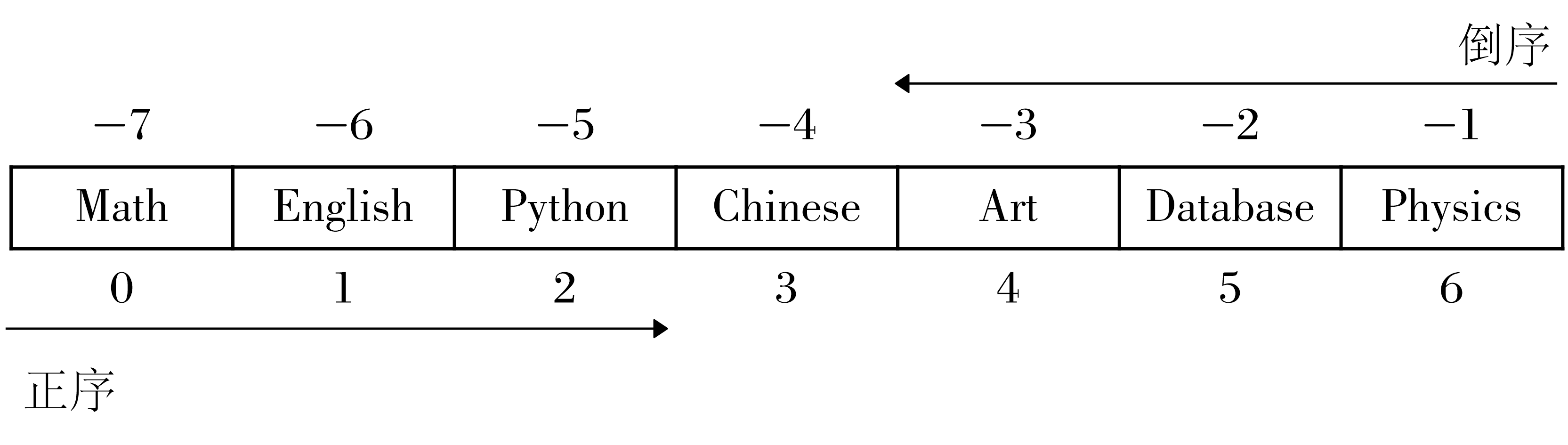
# Code 02 # 数组特性 print(names.ndim) # 数组维度 print(names.size) # 数组元素个数 print(names.dtype) # 数组数据类型 # 数组切片访问 print(names[2]) print(subjects[-3]) # 抽取数组的一部分元素生成新数组称为选择操作 # 方法一:直接以列表形式给出需要的元素索引 print(subjects[[0, 2, 4]]) # 两层括号,[0, 2, 4]为索引列表,外层括号表示元素访问,内层括号表示列表 # 方法二:索引也可表示为start:end:step print(names[1:4]) # 抽取索引为1、2、3的元素 print(subjects[:-1:2]) # 抽取索引为0、2、4的元素。start省略表示从0开始,end省略表示到最后,step省略表示步长为1建立代码块(Cell)Code 02,运行结果如下
1 数组维度 5 数组元素个数 <U6 数组数据类型,其中('<'表示这是一个小端(little-endian)字节序,'U'表示Unicode 字符串,'6'示字符串的最大长度为6个字符。) Potato Art ['Math' 'Python' 'Art'] ['Sheep' 'Potato' 'Donuts'] ['Math' 'Python' 'Art']
Task 3
根据条件筛选数组元素
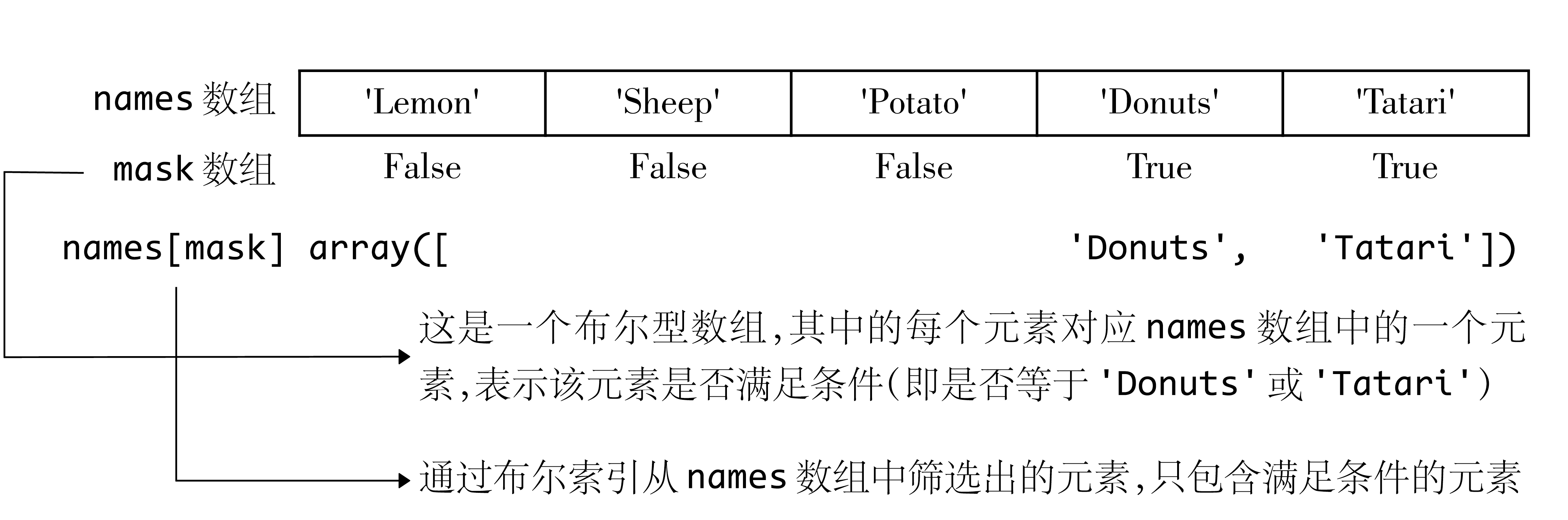
# 使用条件表达式和关系运算符筛选出names数组中值等于“Tatari”或“Donuts”的元素 print(names[(names == 'Tatari') | (names == 'Donuts')]) # 条件表达式:生成布尔型的数组 mask = (names == 'Tatari') | (names == 'Donuts') print(mask) print(names[mask])建立代码块(Cell)Code 03,运行结果如下
['Donuts' 'Tatari'] [False False False True True] ['Donuts' 'Tatari']注释
案例分析 2
Task 1: 新建2-2.ipynb,创建二维数组scores,并记录names中同学subjects的各门考试成绩
由于我们写在一篇文章下的,记它为Code 04吧!
#Code 04 import numpy as np name_list = ['Lemon','Sheep','Potato','Donuts','Tatari'] subject_list = ['Math','English','Python','Chinese','Art','Database','Physics'] score_list = [ [70, 85, 77, 90, 82, 84, 89], [60, 64, 80, 75, 80, 92, 90], [90, 93, 88, 87, 86, 90, 91], [80, 82, 91, 88, 83, 86, 80], [88, 72, 78, 90, 91, 73, 80] ] #冷知识: Py允许在括号、内部进行换行,而不需要显式地使用续/换行符 names = np.array(name_list) subjects = np.array(subject_list) scores = np.array(score_list) scores #直接输出scores的数组输出如下:
array([[70, 85, 77, 90, 82, 84, 89], [60, 64, 80, 75, 80, 92, 90], [90, 93, 88, 87, 86, 90, 91], [80, 82, 91, 88, 83, 86, 80], [88, 72, 78, 90, 91, 73, 80]])访问二维数组元素
建立Code 05,如下所示
#Code 05 print("scores.ndim:", scores.ndim) # 数组维数 print("scores.size:", scores.size) # 数组元素总数,行×列 print("scores.shape:", scores.shape) # 数组的行数和列数 print("scores.dtype:", scores.dtype) # 数组元素的类型输出如下:
scores.ndim: 2 scores.size: 35 scores.shape: (5, 7) scores.dtype: int64给二维数组切片
代码如Code 06所示
#Code 06 a = scores[1,0] b = scores[[1,3],[0,1]] #抽取scores[1,0],scores[3,1] c = scores[[1,3]] #取某行所有列值,可以省略列: d = scores[:, [0,1]] #抽取部分列,行不能省略 e = scores[[0,3], 1:4 ] f = scores[[1,3]][:,[0,1]] #抽取1、3行中0、1列数据,两层选择 print("scores[1,0]:\n", a, '\n') print("scores[[1,3],[0,1]]:\n", b, '\n') print("scores[[1,3]]:\n", c, '\n') print("scores[:, [0,1]]:\n", d, '\n') print("scores[[0,3], 1:4]:\n", e, '\n') print("scores[[1,3]][:,[0,1]]:\n", f, '\n')其中
b = scores[[1,3],[0,1]]的索引方法是花式索引(高级索引),下面对于这个例子给出解释(如果学习了线性代数,理解会比较简单一点,你可以理解为矩阵×向量)b_1 = scores[[1,3]]上述代码
b_1中,通过花式索引[1,4]访问二维数组scores,依次从二维数组scores中获取行索引1、 3对应的元素。之后应当会输出二维数组中行索引为1、3对应的两行元素。如果想要访问二维数组中的部分元素,而不是整行元素,则需要通过两个花式索引完成, 其中第一个花式索引中的整数会被作为行索引,第二个花式索引中的整数会被作为列索引。
当使用两个花式索引操作二维数组时,会按照二维数组的索引方式,依次获取位置相同的行索引和列索引对应的元素,即
b = scores[[1,3]]所以输出结果应当如下:
scores[1,0]: 60 scores[[1,3],[0,1]]: [60 82] scores[[1,3]]: [[60 64 80 75 80 92 90] [80 82 91 88 83 86 80]] scores[:, [0,1]]: [[70 85] [60 64] [90 93] [80 82] [88 72]] scores[[0,3], 1:4]: [[85 77 90] [82 91 88]] scores[[1,3]][:,[0,1]]: [[60 64] [80 82]]
如果对花式索引想有更多的了解,可以先查阅参考链接
创建多维数据的常用方法
arange()等方法使用
np.arange()或np.linspace()创建指定范围的数组。# 创建指定范围的数组 arange_array = np.arange(1, 10, 2) # 步长为2的数组,包含1,不包含10 print("arange数组:", arange_array) # 创建等间隔的数组 linspace_array = np.linspace(1, 10, 5)# 从1到10,共5个数,等间隔 print("linspace数组:", linspace_array)如图所示的代码块,输出结果如下:
arange数组: [1 3 5 7 9] linspace数组: [ 1. 3.25 5.5 7.75 10. ]
reshape()等方法使用
np.reshape()、np.ravel()或np.flatten()改变数组形状。# 创建数组 my_array = np.array([[1, 2, 3], [4, 5, 6]]) # 改变数组形状 reshaped_array = np.reshape(my_array, (3, 2)) print("改变形状后的数组:\n", reshaped_array)这是把2行3列变为3行2列,输出结果如下
改变形状后的数组: [[1 2] [3 4] [5 6]]同理,可以把1维数字转换为指定的多维数组,例如
np.arange(0,15).reshape(3,5)输出结果为
array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14]])
zeros(),ones()等方法使用
np.zeros()、np.ones()、np.full()或np.empty()创建特定填充值的数组。# 创建全零数组 zeros_array = np.zeros((2, 3)) print("全零数组:\n", zeros_array) # 创建全一数组 ones_array = np.ones((2, 3)) print("全一数组:\n", ones_array) # 创建特定填充值数组 full_array = np.full((2, 3), 5) print("特定填充值数组:\n", full_array) # 创建未初始化数组 empty_array = np.empty((2, 3)) print("未初始化数组:\n", empty_array)对于所示的代码,输出结果如下:
全零数组: [[0. 0. 0.] [0. 0. 0.]] 全一数组: [[1. 1. 1.] [1. 1. 1.]] 特定填充值数组: [[5 5 5] [5 5 5]] 未初始化数组: [[1. 1. 1.] [1. 1. 1.]]
案例分析 3
继续在案例分析1、2的基础上进行学习:
- 一维数组访问
a. 在subjects数组中选择并显示序号1、2、4门课的名称,使用负值序号选择并显示names数组中'Potato'
b. 选择并显示names数组从2到最后的数组元素;选择并显示subjects数组2到4的数组元素。
c. 使用布尔条件选择并显示subjects数组中的English和Physics科目名称。- 二维数组访问。
a. 选择并显示scores数组的1、4行。
b. 选择并显示scores数组中行号2、4同学的Math和Python成绩。
c. 选择并显示scores数组中所有同学的Math和Art课程成绩
d. 选择并显示scores数组中“Lemon”的English和“Donuts”的Art课程成绩- 生成由整数10~19组成的2x5的二维数组。
这里给出的示例如下:
# Code 07 Task 1
subject_chosen_124 = subjects[[1,2,4]]
name_chosen_potato = names[-3]
subject_chosen_bool = (subjects == 'English') | (subjects == 'Physics')
subject_chosenb = subjects[subject_chosen_bool]
print(subject_chosen_124)
print(name_chosen_potato)
print(subject_chosen_bool)
print(subject_chosenb)如图所示的代码块,输出结果如下:
['English' 'Python' 'Art']
Potato
[False True False False False False True]
['English' 'Physics']# Code 08 Task 2
score_chosen_14 = scores[[1,4],:]
score_chosen_24 = scores[[2,4]][:,(subjects == 'Math') | (subjects == 'Python')] #在知道名字的情况下等价于下面这个
score_chosen_24_b = scores[(names == 'Potato') | (names == 'Tatari')][:,(subjects == 'Math') | (subjects == 'Python')]
score_shosen_ma = scores[:,(subjects == 'Math') | (subjects == 'Python')]
score_chosen_ld = scores[(names == 'Lemon') | (names == 'Donuts'),(subjects == 'English') | (subjects == 'Art')]
'''
其实这样写也不失为一个好写法?
[(names == 'Donuts'),(subjects == 'Art')]
[(names == 'Lemon'),(subjects == 'English')]
'''
print(score_chosen_14)
print(score_chosen_24)
print(score_chosen_24_b)
print(score_shosen_ma)
print(score_chosen_ld)如图所示的代码块,输出应当如下:
[[60 64 80 75 80 92 90]
[88 72 78 90 91 73 80]]
[[90 88]
[88 78]]
[[90 88]
[88 78]]
[[70 77]
[60 80]
[90 88]
[80 91]
[88 78]]
[85 83]# Code 09 Task 3
np.random.randint(10,19,size=(2,5))如图所示的代码块,输出可能如下:
array([[15, 18, 15, 13, 14],
[10, 13, 11, 11, 11]], dtype=int32)多维数组运算
scores +5 #为所有同学的课程成绩+5分上方操作等价于
a = np.ones((5,7))*5 #创建全是1的5*7数组,每个元素都*5
scores +a #将数组a中的每个元素加到scores数组中对应的元素上二维数组与一维数组运算
# 每个科目基础分不同,为各科目增加相应的基础分
bonus = np.array([3, 4, 5, 3, 6, 7, 2])
scores + bonus
# 修改选定数据
scores[names == 'Tatari', subjects == 'English'] + 5多维数组运算-通用函数
1个输入数组,返回1个数组
| 函数 | 描述 |
|---|---|
| abs、fabs | 计算整数、浮点数或复数的绝对值 |
| sqrt | 计算各元素的平方根 |
| square | 计算各元素的平方 |
| exp | 计算各元素的指数 |
| log、log10 | 自然对数、底数为10的log |
| sign | 计算各元素的正负号 |
| ceil | 计算各元素的ceiling值,即大于等于该值的最小整数 |
| floor | 计算各元素的floor值,即小于等于该值的最大整数 |
| cos、cosh、sin、sinh、tan、tanh | 普通和双曲型三角函数 |
2个输入数组,返回1个数组
| 函数 | 描述 |
|---|---|
| add | 将数据中对应的元素相加 |
| subtract | 从第一个数组中减去第二个数组中的元素 |
| multiply | 数组元素相乘 |
| divide | 数组对应元素相除 |
| power | 对第一个数组中的元素A,根据第二个数组中的相应元素B,计算$A^B$ |
| mod | 元素级的求模运算 |
| copysign | 将第二个数组中的值的符号复制给第一个数组中的值 |
| equal, not_equal | 执行元素级的比较运算,产生布尔型数组 |
聚合函数
支持在行、列or全体数组元素上的聚集函数
| 函数 | 描述 |
|---|---|
| sum | 求和 |
| mean | 算术平均值 |
| min、max | 最大值和最小值 |
| argmin、argmax | 最大值和最小值的索引 |
| cumsum | 从0开始向前累加各元素 |
| cumprod | 从1开始向前累乘各元素 |
随机数组生成模块
np.random模块的主场
| 函数 | 描述 |
|---|---|
| random | 随机产生[0,1)之间的浮点值 |
| randint | 随机生成给定范围内的一组整数 |
| uniform | 随机生成给定范围内服从均匀分布的一组浮点数 |
| choice | 在给定的序列内随机选择元素 |
| normal | 随机生成一组服从给定均值和方差的正态分布随机数 |
案例分析 4
继续在案例分析1、2、3的基础上进行学习:
- 通用函数与聚合函数
a. 将同学的成绩转换成整数形式的十分制分数
b. 统计不同科目的成绩总分
c. 求’Lemon‘所有课程成绩的平均分
d. 查询English成绩最高的同学的姓名- 综合练习
a. 将scores数组中所有同学的英语成绩减去3分并显示
b. 统计scores数组中每名同学所有科目的平均分并显示
c. 使用随机函数生成[-1,1]之间服从均匀分布的3×4二维数组,并计算所有元素的和
# Code 10 Task 1
a = np.floor(scores/10)
b = scores.sum(axis = 0) #按列求和
c = scores[names == 'Lemon'].mean()
d = names[scores[:,subjects == 'English'].argmax()]
for i in [a,b,c,d]:
print(i)可能的输出结果是:
[[7. 8. 7. 9. 8. 8. 8.]
[6. 6. 8. 7. 8. 9. 9.]
[9. 9. 8. 8. 8. 9. 9.]
[8. 8. 9. 8. 8. 8. 8.]
[8. 7. 7. 9. 9. 7. 8.]]
[388 396 414 430 422 425 430]
82.42857142857143
Potato# Code 10 Task 2
for name in names:
average_score = scores[(names == name),:].mean()
print('{}的均分为:{:.2f}'.format(name,average_score))
print (scores)
new_scores = np.subtract(scores[:,subjects == 'English'], 3)
print (new_scores)
random_uniform = np.random.uniform(-1,1,size=(3,4))
print(random_uniform)
print(random_uniform.sum())可能的输出结果是:
Lemon的均分为:82.43
Sheep的均分为:77.29
Potato的均分为:89.29
Donuts的均分为:84.29
Tatari的均分为:81.71
[[70 85 77 90 82 84 89]
[60 64 80 75 80 92 90]
[90 93 88 87 86 90 91]
[80 82 91 88 83 86 80]
[88 72 78 90 91 73 80]]
[[82]
[61]
[90]
[79]
[69]]
[[ 0.91109891 -0.72606825 -0.87901077 -0.8808723 ]
[ 0.21919329 0.54150385 0.71384192 0.38142604]
[ 0.16858705 0.96033454 -0.8466411 0.80976798]]
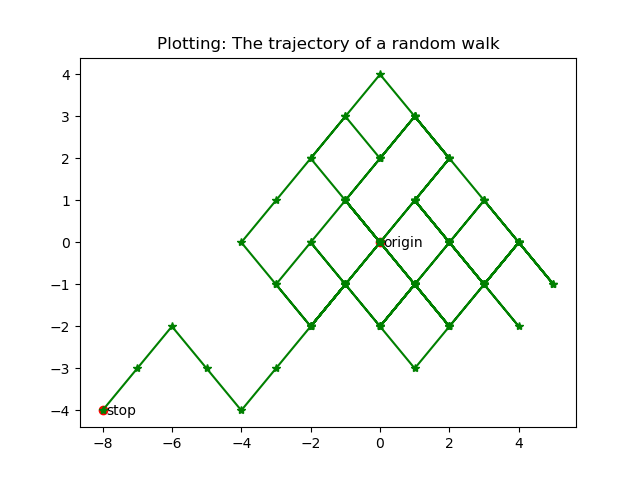
1.3731611543689113案例分析 5 随机游走
随机游走(Random Walk)又称为随机游动或随机漫步,常用来描述花粉的布朗运动与证券的涨跌,我们可以结合NumPy的随机生成函数与ndarray实现随机游走效果:
首先,明确初始位置(0,0),每一步随机地沿着x轴方向左移或右移一个单位,同时沿着y轴方向左移或右移一个单位,且左移或者右移的概率是相等的
那么可以这样考虑:
模拟每步游走方向
- 创建一个2×n的二维数组
- 两行分表表示x,y轴上的运动
- n为移动总步数,每列记录一步
数组元素取值为-1或1(思考:随机整数生成在-1,0,1之间,有3个整数,如何跳掉0?)
- 假设某次随机游走走了10步
import numpy as np
steps = 10
rndwlk = np.random.randint(0, 2, size = (2,steps)) #生成了0~1之间的整数随机数
rndwlk = np.where(rndwlk>0, 1, -1)
rndwlk注:np.where()
rndwlk = np.where(rndwlk > 0, 1, -1)- rndwlk > 0:这是一个条件表达式,用于检查数组 rndwlk 中的每个元素是否大于 0。
- 1:如果条件为真(即某个元素大于 0),则将该元素替换为 1。
- -1:如果条件为假(即某个元素不大于 0,也就是小于等于 0),则将该元素替换为 -1。
- rndwlk = ...:最终,将处理后的结果重新赋值给变量 rndwlk。
输出可能如下:
array([[-1, 1, 1, 1, 1, 1, 1, -1, -1, 1],
[-1, 1, -1, 1, -1, -1, -1, -1, 1, -1]])计算每步游走后的位置
- 第n步的位置为前n-1步位置+第n步
- 累加和函数
cumsum()
position = rndwlk.cumsum(axis = 1) #逐列求累加和
position输出可能如下:
array([[-1, 0, 1, 2, 3, 4, 5, 4, 3, 4],
[-1, 0, -1, 0, -1, -2, -3, -4, -3, -4]], dtype=int32)计算每步游走后距原点距离
- 平面距离计算$\sqrt{x^2+y^2}$
- 累加和函数
cumsum()
dists = np.sqrt(position[0]**2 + position[1]**2) #sqrt求平方根
np.set_printoptions(precision=4) #设置环境中保留4位小数
dists输出可能如下:
array([ 1.4142, 0., 1.4142, 2. , 3.1623, 4.4721,
5.8310, 5.6569, 4.2426, 5.6569])当然,你还可以求以下变量
>>> dists.max() #游走最远距离
5.8310>>> dists.min() #游走最近距离
0.0>>> dists.mean() #游走平均距离
3.3850(dists>dists.mean()).sum() #超出平均距离的次数
5重复多次随机游走过程,物体距离原点距离的变化趋势是什么?
观察得步数越多,物体距离原点的平均距离会越远
- 【后期学习】可视化
这里仅展示课堂上的可视化代码
#为轨迹序列增加起始原点
x = np.append(0, position[0])
y = np.append(0, position[1])
#绘制图形
import matplotlib.pyplot as plt
plt.plot(x,y, c='g',marker='*') #画折线图
plt.scatter(0,0,c='r',marker='o') #画原点
plt.text(.1, -.1, 'origin') #添加原点说明文字
plt.scatter(x[-1],y[-1], c='r', marker='o') #单独画终点
plt.text(x[-1]+.1, y[-1]-.1, 'stop') #添加终点说明文字
plt.title('Plotting: The trajectory of a random walk') #添加图题
plt.show() #显示图效果可能如下:
Exercise 1
- 编写Python程序实现以下功能:从键盘输入若干同学的姓名.保存在字符串列表中:
输入某个同学的名字,检索是否已保存在列表中。
#H1-1
name_list = []
print('空回车查看当前成员列表')
while True:
name_input = input('请输入姓名:')
if name_input in name_list:
print('已存在该同学,请重试')
elif name_input == '':
print(name_list)
else:
name_list.append(name_input)
- 编写Python程序实现以下功能:使用字典记录多位同学的姓名及对应身高:
输入任意同学的姓名,在字典中查找并显示所有高于此身高的同学信息。
#H1-2
name_dic={}
print('空回车查看当前字典')
print('请按以下格式录入:姓名+身高')
print('如:小明+167')
print('直接输入姓名查找并显示所有高于此身高的同学信息')
while True:
name_input = input('请输入:')
if '+' in name_input:
name_list = name_input.split('+')
name_dic[name_list[0]] = name_list[1]
elif name_input == '':
print(name_dic)
else:
if name_input in name_dic:
common_height = name_dic.get(name_input)
count = 0
for name,height in name_dic.items():
if height > common_height:
print('{}\t{}'.format(name,height))
count = count + 1
else:
continue
if count == 0:
print('没有比{}更高的同学了'.format(name))
else:
print('该同学不在字典里,请重试')
Exercise 2
- “大润发”、“沃尔玛”、“联华”和“农工商”四个超市都卖苹果、香蕉、桔子和芒果四种水果。使用NumPy的ndarray实现以下功能:
a) 创建2个一维数组分别存储超市名称和水果名称;
b) 创建1个4×4的二维数组存储不同超市的水果价格,其中价格由4到10范围内的随机数生成;
c) 选择“大润发”的苹果和“联华”的香蕉,并将价格增加1元;
d) “农工商”水果大减价,所有水果价格减少2元;
e) 统计四个超市苹果和芒果的销售均价;
f) 找出桔子价格最贵的超市名称(不是编号)。
#Cell 01
import numpy as np
# Task A 创建2个一维数组分别存储超市名称和水果名称;
shop_list=['大润发','沃尔玛','联华','农工商']
fruit_list=['苹果','香蕉','桔子','猕猴桃','芒果']
shops = np.array(shop_list)
fruits = np.array(fruit_list)#Cell 02
# Task B 创建1个4×4的二维数组存储不同超市的水果价格,其中价格由4到10范围内的随机数生成;
price = np.random.randint(4,10,(4,5))
print(price)#Cell 03
# Task C 选择“大润发”的苹果和“联华”的香蕉,并将价格增加1元;
price [(shops == '大润发'),(fruits == '苹果')] += 1
price [(shops == '联华'),(fruits == '香蕉')] += 1
print(price)#Cell 04
# Task D “农工商”水果大减价,所有水果价格减少2元;
price [(shops == '农工商'),:] -= 2
print(price)#Cell 05
# Task E 统计四个超市苹果和芒果的销售均价;
for kind in ['苹果','芒果']:
average_price = price[:,(fruits == kind)].mean()
print('{}的均价为:{}'.format(kind,average_price))
#Cell 06
# Task F 找出桔子价格最贵的超市名称(不是编号)。
shop_index = price[:,(fruits == '桔子')].argmax()
most_gui = shops[shop_index]
print('最贵的超市是:',most_gui)
- 基于随机游走实例,使用ndarray和随机数生成函数模拟一个物体在三维空间随机游走的过程。
a)创建3×10的二维数组,记录物体每一步在三个轴向上的移动距离。在每个轴向的移动距离服从标准正态分布(期望为0,方差为1)。行序0、1、2分别对应x、y和z轴;
b)计算每一步走完后物体在三维空间的位置;
c)计算每一步走完后物体距离原点的距离;
d)统计物体在z轴上到达的最远距离;(提示:使用abs()绝对值函数对z轴每一步运动后的位置求绝对值,然后求最大距离)
e)统计物体在三维空间距离原点的最近距离值。
#Cell 01
import numpy as np
# 更改输出模式,使所有NumPy输出结果保留两位小数喵( •̀ ω •́ )✧
# np.set_printoptions(formatter={'float': '{:0.2f}'.format})
# Task 1 创建3×10的二维数组,记录物体每一步在三个轴向上的移动距离。在每个轴向的移动距离服从标准正态分布(期望为0,方差为1)。行序0、1、2分别对应x、y和z轴;
dimension = np.array(['dx','dy','dz'])
steps = 10
rndwalk = np.random.normal(0,1,size=(3,10))
print (rndwalk)#Cell 02
# Task 2 计算每一步走完后物体在三维空间的位置;
position = rndwalk.cumsum(axis = 1)
print(position)#Cell 03
# Task 3 计算每一步走完后物体距离原点的距离;
distance = np.sqrt(np.square(position[0]) + np.square(position[1] + np.square([position[2]])))
print(distance)
# 提示:power(m,n)可以用来求m^(n)运算#Cell 04
# Task 4 统计物体在z轴上到达的最远距离;(提示:使用abs()绝对值函数对z轴每一步运动后的位置求绝对值,然后求最大距离)
z_distance = np.abs(rndwalk[(dimension == 'dz'),:])
z_dist_max = z_distance.max()
print('在z轴达到的最远距离是:',z_dist_max)#Cell 05
# Task 5 统计物体在三维空间距离原点的最近距离值。
distance_min = np.abs(position).min()
print('3维空间内距离原点最短的距离是:',distance_min)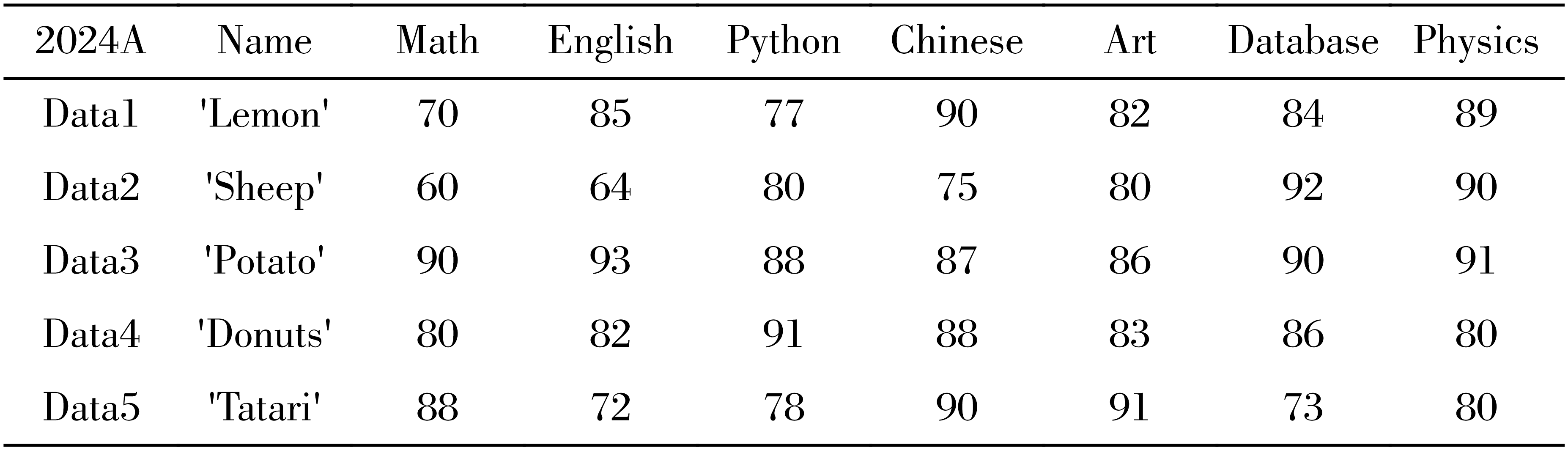
2 条评论
作者以简洁明了的语言,传达了深刻的思想和情感。
遇事不决,可问春风;春风不语,即随本心。∠( ᐛ 」∠)_
——钟部